1. Metadata
IRI |
|
Spatial Uncertainty for Features & Functions (SUFF) Model |
|
A Semantic Web model that builds on elements of the GeoSPARQL 1.1 ontology to represent uncertainty in the location of geometric features, supporting cartographic representations as well as analytical functions. |
|
2024-03-15 |
|
2024-08-07 |
|
2024-03-15 |
|
This profile of GeoSPARQL was made to satisfy various projects' needs in 2023 - 2024 |
|
0.0.2 |
|
© Nicholas J. Car, 2024 |
|
Machine-readable form (RDF) |
2. Preamble
2.1. Abstract
This is a Semantic Web model that builds on elements of the GeoSPARQL 1.1 ontology to represent uncertainty in the location of geometric features, supporting cartographic representations as well as analytical functions.
2.2. Namespaces
This model uses the GeoSPARQL 1.1 namespace and those of several others from well-known and mostly standardised ontologies as well as its own - suff. All namespaces used, and prefixes for them, are listed in the table below.
| Prefix | Namespace | Description |
|---|---|---|
|
This model |
|
|
Levels of Measurement vocabulary namespace |
|
|
Non-resolving namespace for examples |
|
|
GeoSPARQL Ontology Namespace |
|
|
GeoSPARQL Functions Namespace |
|
|
Web Ontology Language ontology |
|
|
RDF Schema ontology |
|
|
Sensor, Observation, Sample, and Actuator ontology |
|
|
schema.org model |
|
|
Simple Knowledge Organization System (SKOS) ontology |
|
|
Time Ontology in OWL |
|
|
Vocabulary of Interlinked Data (VoID) ontology |
|
|
XML Schema Definitions ontology |
2.3. Conformance
This model’s specification conforms to the OntPub Profile which is a standard for ontology publication that mandates certain structural and metadata properties for the model as a whole and model elements.
3. Introduction
This model defines ways of arranging models elements from GeoSPARQL, other common Semantic Web models such as schema.org, and some of its own elements to represent uncertainty in the location of geospatial features.
For example, a region with a broad boundary (also called an indeterminate boundary, see BURROUGH-FRANK) is among the most fundamental representations of uncertainty in location. The figure below shows a simple example of such a region: the red central core is regarded as definitely in the region; the pink penumbra is possibly in the region; and everything else is definitely not in the region.
Such representations are widely used in various simple models of uncertainty, including rough sets (WORBOYS-CEUS) and the so-called "egg-yolk model" of indeterminate RCC (region connection calculus) regions (COHN-GOTTS). The listing below provides the example data for the figure above.
PREFIX : <https://w3id.org/suffer/>
PREFIX ex: <http://example.com/>
PREFIX geo: <http://www.opengis.net/ont/geosparql#>
PREFIX rdfs: <http://www.w3.org/2000/01/rdf-schema#>
PREFIX schema: <https://schema.org/>
PREFIX xsd: <http://www.w3.org/2001/XMLSchema#>
ex:indeterminate-boundary-region
a geo:Feature ;
schema:name "Region with indeterminate boundary" ;
:hasGeometries [
a geo:GeometryCollection ;
rdfs:_1 [
a geo:Geometry ;
schema:name "Definitely in" ;
geo:asWKT "..."^^geo:wktLiteral ;
] ;
rdfs:_2 [
a geo:Geometry ;
schema:name "Possibly in" ;
geo:asWKT "..."^^geo:wktLiteral ;
] ;
] ;
.The idea may be extended in a variety of different ways. For example, the following figure and code listing provide graphical and data views of a more complex uncertain feature created according to this model.
PREFIX : <https://w3id.org/suffer/>
PREFIX ex: <http://example.com/>
PREFIX geo: <http://www.opengis.net/ont/geosparql#>
PREFIX rdfs: <http://www.w3.org/2000/01/rdf-schema#>
PREFIX schema: <https://schema.org/>
PREFIX xsd: <http://www.w3.org/2001/XMLSchema#>
ex:indigenous-homeland-x
a geo:Feature ;
schema:name "Indigenous Homeland X" ;
:hasGeometries [
a geo:GeometryCollection ;
rdfs:_1 [
a geo:Geometry ;
schema:name "A" ;
geo:asWKT "..."^^geo:wktLiteral ;
] ;
rdfs:_2 [
a geo:Geometry ;
schema:name "B" ;
geo:asWKT "..."^^geo:wktLiteral ;
] ;
rdfs:_3 [
a geo:Geometry ;
schema:name "C" ;
geo:asWKT "..."^^geo:wktLiteral ;
] ;
rdfs:_4 [
a geo:Geometry ;
schema:name "D" ;
geo:asWKT "..."^^geo:wktLiteral ;
] ;
] ;
.The following subsection in this Introduction describes the motivation for this work and the final subsection describes the structure of this specification.
3.1. Motivation
Representing uncertainty in location is one of the most longstanding—and tricky—topics in geographic information science. Many practical applications have the need to represent features with uncertain locations, including representing:
-
the occurrence of mineral deposits, where the limitations of borehole sampling and interpolation may lead to uncertainty about the correct value at a location (inaccuracy)
-
the occurrence of endangered species, where the exact location may need to be obscured for legal reasons and in order to protect endangered native species from damage or interference (imprecision)
-
the traditional lands of First Nations people, which are intrinsically not definable by precise, measurable extents, and so representation by a region with a crisp boundary is not sensible (vagueness).
These three examples relate to the three fundamental types of "imperfection" (uncertainty) in spatial data defined in WORBOYS-CLEMENTINI: inaccuracy (errors or a lack of correctness in data); imprecision (a lack of detail/exactness in data); and vagueness (a special case of imprecision, where precise boundaries between concepts remain ill-defined). Many other subtypes of uncertainty (such as bias, completeness, ambiguity, granularity, see DUCKHAM-BOOK) can be defined in terms of these three fundamental types, summarized in the figure below.
3.2. Structure
GeoSPARQL defines spatial Features and Geometry classes that can be used, with elements from other well-known Semantic Web models, for data with uncertainty in all the above scenarios. However, without dedicated methods for this, the representation and handling of it will differ in different implementations.
Consequently, this model provides:
-
Principles: A series of principles describing the scope of what this model is intending to offer
-
Elements: New Semantic Web Classes and Predicates defined here and guided reuse of Classes and Predicates from other models to represent uncertainty
-
Rules: A series of rules that must be followed in the use of the elements of this model to ensure consistency in implementation
-
Topological Functions: Definitions for topological functions that can be performed on spatial data with uncertainty, as represented by the Elements of this model in accordance with this model’s Rules
Further, the model provides a Geometry Collection class which can be used to associate multiple geometries with a feature. This is the core of this model since multiple geometries for a feature can be used to convey location uncertainty in several ways - see the Principles below.
GeoSPARQL 1.1 does not, however, provide all the elements needed for deterministic representations of feature location uncertainty, nor does GeoSPARQL 1.1 describe how to perform topological functions on features with uncertain location representation. This model defines conventions for GeoSPARQL 1.1 element use, and introduces several new model elements, for this purpose.
Where spatial uncertainty is handled in mainstream non-Semantic Web GIS today, such as ESRI’s ArcGIS[1], it is generally handled only cartographically and then only superficially - in the display of the data, not encoded within the data. This leads to the issue of reproducibility, where cartographic representations are not precisely defined, persistently stored, or reproducible on other systems.
By contrast, this model encodes uncertainty in the data itself. Together with the rules presented in the Principles section, the model can provide a basis for any software system to display uncertainty cartographically or analyse uncertainty spatially (such as probabilstic topological interactions).
4. Principles
This section give a series of principles describing the scope of what this model is aims to offer.
4.1. Uncertainty in location, represented using geometry
This model only directly addresses the representation of uncertainty in the location of spatial features, where that uncertainty can be captured using a set of geometries.
The model does not address uncertainty in the values of other attributes or properties of features. Other ontologies do exist to provide for the representation of measurement uncertainty, including simple models such as schema.org include properties such as marginOfError for this purpose.
Further, this model is not intended to be used to represent uncertainty in location when a simple property associated with a single geometry would suffice. Such simple representations are already accessible through elements from GeoSPARQL, see:
4.2. Core mechanism
Uncertainty in the location of a feature is captured by linking the feature not to one geometry but to multiple - a geometry collection. Each geometry in the collection conveys part of the representation of the feature’s location together with a value either being given in the data or inferrable due to the geometry’s relative position in the collection.
The interpretation of the value is partly captured through three levels of measurement, as follows.
4.2.1. Levels of measurement
The SUFF model recognises three levels of measurement[2] as defined in the Levels of Measurement vocabulary in the [Supporting Vocabularies] section of this model.
The three levels defined are:
The level of measurement will be indicated either directly by the predicate level of measurement on a Geometry Collection instance, or it will be divined from other properties of the geometries. The default value is Nominal.
4.3. Approximate topological relations
The GeoSPARQL standard provides both an ontology which defines spatial elements and predicates to indicate topological relationships between them and also function definitions that can be used to calculate those predicates.
For example, the predicate geo:sfWithin indicated that its subject is spatially within its object where within is the Simple Features Within relation defined by OGC-06-103r4. The related GeoSPARQL function is geof:sfWithin which defines the parameters and results from the function used to calculate the `geo:sfWithin relation between two spatial objects.
One objective of this model is to enable the definition of rules that propagate uncertainty in location through to levels of certainty in topological relation. There are an enormous range of different possibilities when computing such a relation in the literature, including COHN-GOTTS, CLEMENTINI-FELICE, BJORKE, WINTER, ROY-STELL to name but a few.
4.3.1. Minimal method for approximate topological relation computation
For example, the COHN-GOTTS model of indeterminate regions distinguishes 46 topologically distinct relations between egg-yolk regions (see below).
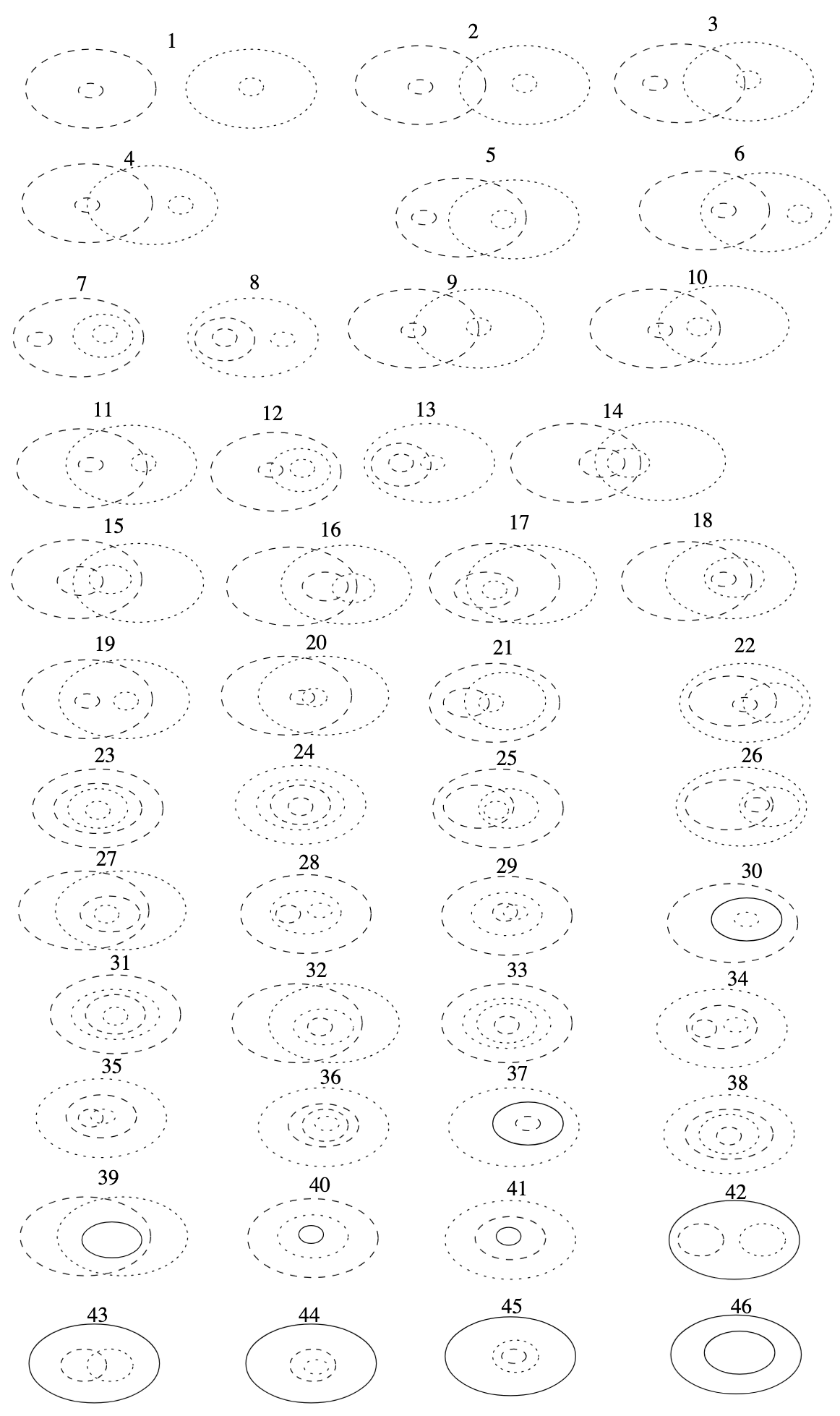
In turn, this results in 13 distinct clusters of RCC5 relations between two egg yolk regions, given all possible "precisifications" of their boundaries, shown below.
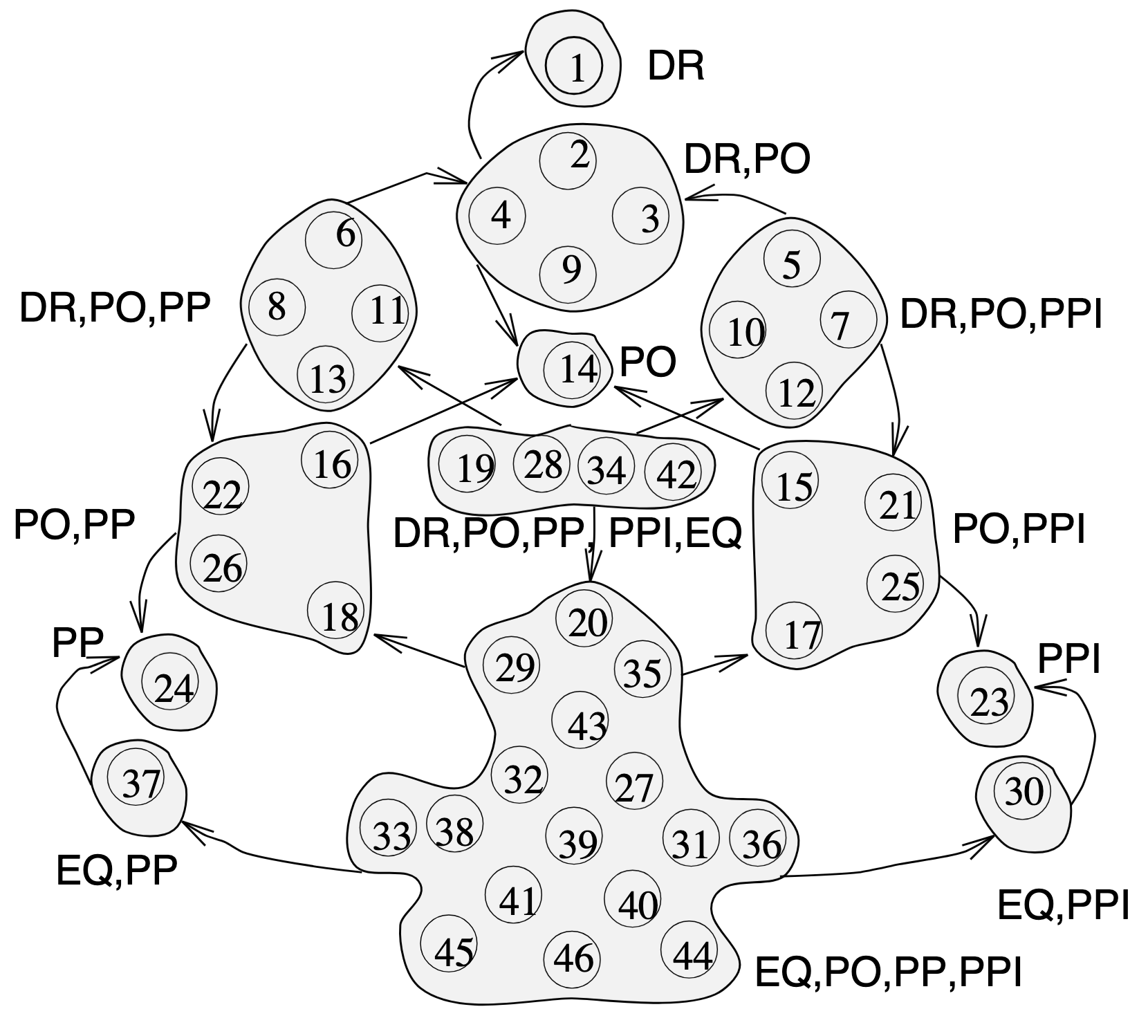
Based on this result, a minimal method for topological relation computation based on the simple egg-yolk model of indeterminate regions by and adopting a simple three-valued interpretation of "intersects" (i.e., definitely intersects, possibly intersects, definitely doesn’t intersect) is as follows:
Given twe egg-yolk regions A and B
-
Compute the unique topological relation R between A and B (numbered 1 .. 46)
-
If R is in {1} then A definitely doesn’t intersect B
-
If R is in {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 19, 28, 34, 42} then A possibly intersects B
-
Else A definitely intersects B
-
5. Elements
This section defines the data elements of this model.
This model is composed of Web Ontology Language (OWL) OWL Classes, Predicates and classification vocabularies. While some predicates are restricted in their use to various classes, the Classes and Predicates are actually defined individually and both are "first class model citizens", with global identity, that can be used in isolation and together. This is in contrast to Unified Modelling Language (UML) Class Diagrams which treat most Predicates as element of particular Classes.
This model defines only a few Classes, Predicates and Vocabularies but reuses many from other models. Where it does, basic details of a reference to that Class or Predicates' definition via rdfs:isDefinedBy, and a scope note about using it in this model are given.
5.1. Classes
5.1.1. Classes defined by this model
-
??
Address
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
Address |
Definition |
The Address class represents structured information that allows unambiguous identified of an object for the purposes of identification and location |
Is Defined By |
This model |
Subclass Of |
|
Provenance |
Derived from [ISO19160-1]'s |
Expected Predicates |
|
Example |
|
5.1.2. Existing classes reused by this model
Feature
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
Feature |
Definition |
A discrete spatial phenomenon in a universe of discourse |
Is Defined By |
|
Scope Note |
Used as the basis for the Road Object class |
Geometry
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
Geometry |
Definition |
A coherent set of direct positions in space. The positions are held within a Spatial Reference System (SRS). |
Is Defined By |
|
Scope Note |
Used to give spatial representation information for a Road Object |
GeometryCollection
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
Geometry Collection |
Definition |
A collection of individual Geometries |
Is Defined By |
Concept
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
Concept |
Definition |
An idea or notion; a unit of thought |
Is Defined By |
|
Scope Note |
Used to indicate a value that should come from a vocabulary (modelled as a `skos:ConceptScheme) |
5.2. Predicates
5.2.1. Predicates defined by this model
hasGeometries
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
has geometries |
Definition |
Indicates a collection of spatial representations for a given Feature |
Is Defined By |
This model |
Domain |
|
Range |
5.2.2. Existing predicates reused by this model
hasGeometry
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
has geometry |
Definition |
A spatial representation for a given Feature |
Is Defined By |
|
Domain |
|
Range |
|
Scope Note |
Used to indicate the Geometry of a Feature, such as a Road Object |
member
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
member |
Definition |
A member of the subject resource |
Is Defined By |
|
Domain |
|
Range |
|
Scope Note |
In the SUFF Model, use this predicate to indicate the member Geometry instances within a GeometryCollection |
_1
| Property | Value |
|---|---|
IRI |
|
Preferred Label |
firs member |
Definition |
An instance of the rdfs:ContainerMembershipProperty indicating the first member in a collection |
Is Defined By |
|
Subproperty Of |
|
Scope Note |
In the SUFF Model, use this predicate to indicate the first member Geometry instance within an ordered GeometryCollection |
5.3. Vocabularies
This model uses a vocabulary of Levels of Measurement to provide values for the range of the predicate level of measurement. that vocabulary is published online at https://linked.data.gov.au/def/levels-of-measurement.
A simple listing of that vocabulary is also given below.
5.3.1. Levels of Measurement
| IRI | Preferred Label | Definition |
|---|---|---|
nominal |
The nominal level differentiates between items or subjects based only on their names or (meta-)categories and other qualitative classifications they belong to; thus dichotomous data involves the construction of classifications as well as the classification of items |
|
ordinal |
The ordinal level allows for rank order (1st, 2nd, 3rd, etc.) by which data can be sorted but still does not allow for a relative degree of difference between them |
|
interval |
The interval type allows for defining the degree of difference between measurements, but not the ratio between measurements |
|
ratio |
The ratio type takes its name from the fact that measurement is the estimation of the ratio between a magnitude of a continuous quantity and a unit of measurement of the same kind |
Bibliography
- AS4189:2011
-
Standards Australia. AS/NZS 4819:2011 Rural and urban addressing
- BJORKE
-
Bjørke, J.T. Topological relations between fuzzy regions: Derivation of verbal terms. Fuzzy sets and systems 141.3 (2004): 449-467.
- BURROUGH-FRANK
-
Burrough, P.A. and Frank, A.U. (Eds.) Geographic Objects with Indeterminate Boundaries. CRC Press: Boca Raton, FL (1996). https://doi.org/10.1201/9781003062660
- CNM
-
Australian Government Linked Data Working Group. Compound Naming Model. Semantic Web data model (2023). https://linked.data.gov.au/def/cn
- CLEMENTINI-FELICE
-
Clementini, E. and Di Felice, P. Approximate topological relations. International Journal of Approximate Reasoning 16.2 (1997): 173-204.
- COHN-GOTTS
-
Cohn, A.G. and Gotts, N.M. The "egg-yolk" representation of regions with indeterminate boundaries. In Geographic objects with indeterminate boundaries. CRC Press (1996). 171-187.
- DUCKHAM-BOOK
-
Duckham, M., Sun, Q.C., Worboys, M.F., GIS: A computing perspective, 3rd Ed. CRC Press: Boca Raton, FL (2023). http://doi.org/10.1201/9780429168093
- CONNEGP
-
World Wide Web Consortium, Content Negotiation by Profile, W3C Working Draft (20 March 2022). https://w3c.github.io/dx-connegp/connegp/
- GEO
-
Open Geospatial Consortium, OGC GeoSPARQL - A Geographic Query Language for RDF Data, Version 1.1 (2021). OGC Implementation Specification. http://www.opengis.net/doc/IS/geosparql/1.1
- GNAF
-
Geoscape Australia. Geocoded National Address File, G-NAF (2023). https://data.gov.au/dataset/ds-dga-19432f89-dc3a-4ef3-b943-5326ef1dbecc
- GN
-
Queensland Spatial Information. Geographical Names Model (2023). https://linked.data.gov.au/def/gn
- ISO-IEC-14977
-
International Organization for Standardization, ISO/IEC 14977 : 1996(E): Extended Backus–Naur form. International Organization for Standardization (1996). https://www.cl.cam.ac.uk/~mgk25/iso-14977.pdf
- ISO19101-1
-
International Organization for Standardization, ISO 19101-1:2014 Geographic information — Reference model — Part 1: Fundamentals (2014)
- ISO19125-1
-
International Organization for Standardization, ISO 19125-1: Geographic information — Simple Feature Access - Part 1: Common Architecture (2004)
- ISO19156
-
International Organization for Standardization, ISO 19156: Geographic information — Observations and measurements (2011)
- KIRCH
-
Kirch, W. (eds), Level of Measurement (2008). In: Encyclopedia of Public Health. Springer, Dordrecht. https://doi.org/10.1007/978-1-4020-5614-7_1971
- OGC-06-103r4
-
Open Geospatial Consortium: OGC 06-103r4 OpenGIS® Implementation Standard for Geographic information — Simple feature access — Part 1: Common architecture. http://www.opengis.net/doc/is/sfa/1.2.1
- OWL
-
World Wide Web Consortium, OWL 2 Web Ontology Language Document Overview (Second Edition), W3C Recommendation (11 December 2012). https://www.w3.org/TR/owl2-overview/
- PROF
-
World Wide Web Consortium, The Profiles Vocabulary, W3C Working Group Note (18 December 2019). https://www.w3.org/TR/dx-prof/
- PROV
-
World Wide Web Consortium, The Profiles Vocabulary, W3C Working Group Note (18 December 2019). https://www.w3.org/TR/dx-prof/
- RDF
-
World Wide Web Consortium, RDF 1.1 Concepts and Abstract Syntax, W3C Recommendation (25 February 2014). https://www.w3.org/TR/rdf11-concepts/
- RDFS
-
World Wide Web Consortium, RDF 1.2 Schema, W3C First Public Working Draft (16 May 2023). https://www.w3.org/TR/rdf12-schema/
- ROY-STELL
-
Roy, A.J. and Stell, J.G. Spatial relations between indeterminate regions. International Journal of Approximate Reasoning 27.3 (2001): 205-234.
- SDO
-
W3C Schema.org Community Group, schema.org. Community ontology (2015). https://schema.org
- SHACL
-
World Wide Web Consortium, Shapes Constraint Language (SHACL), W3C Recommendation (20 July 2017). https://www.w3.org/TR/shacl/
- SSN
-
World Wide Web Consortium, Semantic Sensor Network Ontology, W3C Recommendation (19 October 2017). https://www.w3.org/TR/vocab-ssn/
- SKOS
-
World Wide Web Consortium, SKOS Simple Knowledge Organization System Reference, W3C Recommendation (18 August 2009). https://www.w3.org/TR/skos-reference/
- TTL
-
World Wide Web Consortium, RDF 1.1 Turtle Terse RDF Triple Language, W3C Recommendation (25 February 2014). https://www.w3.org/TR/turtle/
- WINTER
-
Winter, S. Uncertain topological relations between imprecise regions. International Journal of Geographical Information Science 14.5 (2000): 411-430.
- WORBOYS-CEUS
-
Worboys, M.F., Computation with imprecise geospatial data. Computers, Environment and Urban Systems 22.2 (1998): 85-106. https://doi.org/10.1016/S0198-9715(98)00023-4
- WORBOYS-CLEMENTINI
-
Worboys, M.F. and Clementini, E., Integration of imperfect spatial information. Journal of Visual Languages & Computing 12.1 (2001): 61-80.https://doi.org/10.1006/jvlc.2000.0187
- XSD
-
World Wide Web Consortium, XML Schema Part 2: Datatypes, Second Edition, W3C Recommendation (28 October 2004). http://www.w3.org/TR/xmlschema-2/.